 おまけ解説
おまけ解説 おまけ解説
おまけ解説 課題:
強制振動の方程式を,Runge-Kutta(4次)法で数値的に解くこと
課題:
強制振動の方程式を,Runge-Kutta(4次)法で数値的に解くこと
初期条件:
t=0〜150まで適当な時間刻み h で順次数値解をもとめる。
常微分方程式の数値解法は,1階の常微分方程式を基本としている。
変換はいろいろ考えられるであろうが,
2連の常微分方程式
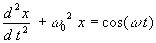
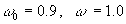
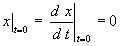
 前処理:
1階常微分方程式への変換
前処理:
1階常微分方程式への変換
したがって,上の2階の方程式を,
まず,1階の連立常微分方程式の形に変換しなければならない。
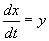
とおくのが最も一般的である。
そうすると,上の式は次のような形に書きなせる。
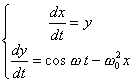
 ルンゲクッタの4次公式
ルンゲクッタの4次公式
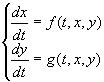
を数値的に解く,つまり,t のある時点 tn における
xn,
yn の値があたえられたとき,
h だけ進んだつぎの
tn+1 = tn+h の時点の値
xn+1,yn+1 は,
つぎの式で近似的に計算できる。
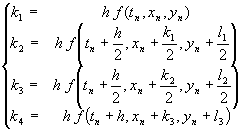
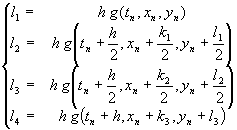
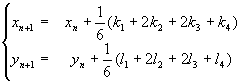
これが,ルンゲクッタの4次公式である。
精度良く計算するためには,時間刻みhはあまり大きくとれない。
 戻る
戻る
平成15年12月03日更新