最終課題 最終課題＜ 重力三体問題 ＞
３つの天体A,B,Cが，互いに万有引力を及ぼしあいながら，２次元平面内を運動するときの，軌道を予測するプログラムを完成してください。適当な初期条件のもと，実際に軌道計算を行って，その結果を図示してください。
この問題の支配方程式は，以下のとおりになります。ここで，m は各天体の質量，(x,y) は各天体の2次元位置，r は２天体間の距離で，それぞれの添え字が対応する天体を表わします。
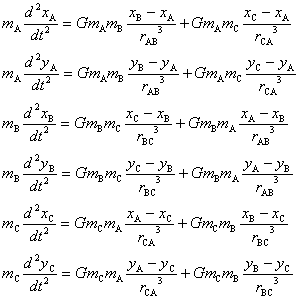
よく知られているように，三体問題は解析的に解くことはできず，数値計算によってしか解を得ることができないのです。いわゆる，連立常微分方程式の初期値問題ですから，前に解説したとおり，ルンゲ・クッタ法などを利用することになります。
なお，単位系としては，距離，質量をそれぞれ，天文単位（地球と太陽の距離＝1.49597870*10^11 m）と太陽の質量（1.9891*10^30 kg）を基準とし，時間は日で計算するようにしてください。
因みに，次のような初期条件（t=0 における各天体の位置と速度）で軌道を計算すると，図のような軌道が得られます。ここで，G は重力定数（上に述べた単位系での値），Ts は１太陽年です。
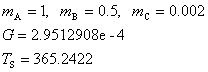
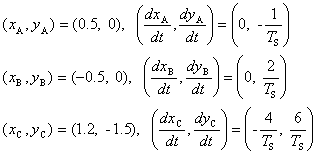
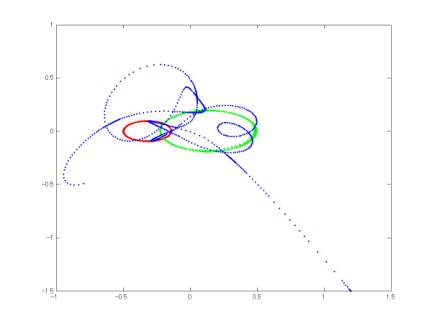
連星系（太陽と同じ質量の赤い恒星とその半分の質量の緑の恒星）に，外部から彗星（青色）が飛来してきた状況を，計算したもので，とても複雑な軌道になることがわかります。君たちが作成したプログラムで，これと同じ計算しても，上の図と同じ結果が得られるとは限りません。この問題は，初期値のちょっとした差異にも，また，計算誤差にも非常に敏感なのです。（つまり，正確な軌道計算は非常に難しいということです。）
何か面白い図になるように，異なる質量比や初期条件について試してください。
＜ ２次元ラプラス方程式の解 ＞
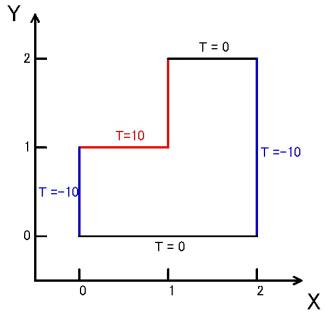
図のような２次元領域があり，その周囲の温度が，図中に示したように保たれているものとします。内部の温度分布を差分法で求め，等高線でその温度分布を図示しなさい。
この問題の支配方程式は，温度分布を T(x,y) として，以下のような，ラプラス方程式になります。この問題の場合，温度分布は，対象領域の大きさや熱伝導率などには依存しません。またこの問題は，なにも温度分布に限ったものではなく，たとえば電位分布なども同じ支配方程式になります。
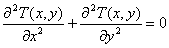
支配方程式を，差分近似で解くことを考える。対象領域内の温度分布を，格子点 (i凅,j凉) 上で求めるものとすると，温度分布 T(i凅,j凉)=Ti,j の満足する方程式は，以下のようになります。
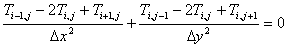
凅=凉=1 とすると，単純に以下のようになります。
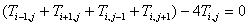
この式から明らかなように，ある格子点 (i,j) の温度は，隣接する４点 (i-1,j),(i+1,j),(i,j-1),(i,j+1) の温度と関係しています。境界以外の全ての格子点でこのような差分近似式を立てることになるので，温度分布を求めることは，領域内部の全ての格子点における温度を未知数とした連立１次方程式を解く問題となります。
分割は，１０〜２０程度で結構です。なお，Gaussの消去法など連立一次方程式の解法については，自分で調べてください。また，違う境界条件について解析してもらっても結構です。これにこだわる必要はありませんが，たとえば，下記のような温度分布図を作ってください。
＜ 波動方程式の差分解法 ＞
1次元波動方程式に対して，次のような条件が与えられているとき，
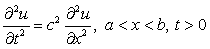
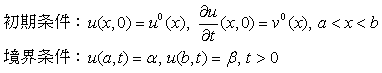
これを有限差分解析で近似計算することを考える。
いま，区間a≦x≦b 内に次のような等間隔の離散点xj を
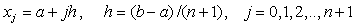
定義し，また時間についても，微小時間間隔Δt を導入して
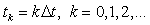
と定める。さらに，時間tk での離散点xj における関数値をukj と表記する。
さて，波動方程式と，初期条件および境界条件を
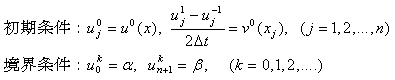
のように差分近似で与えることにする。ただし，Δt とh の間には，
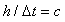なる関係が満足されているものとする。
(詳細は説明しないが，計算の近似精度が比較的良くなるという理由からである。)
さて，この解法を用いて，区間 0≦x≦1 で，
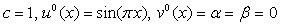
の場合の近似解を計算し，厳密解
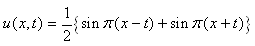
と比較しなさい。また，離散点数，経過時間tk，コンピュータプログラムでの実数変数および実数計算の有効桁数(単精度であるか倍精度であるか)などの因子が，計算値と厳密解の差に及ぼす影響を調べ，考察しなさい。
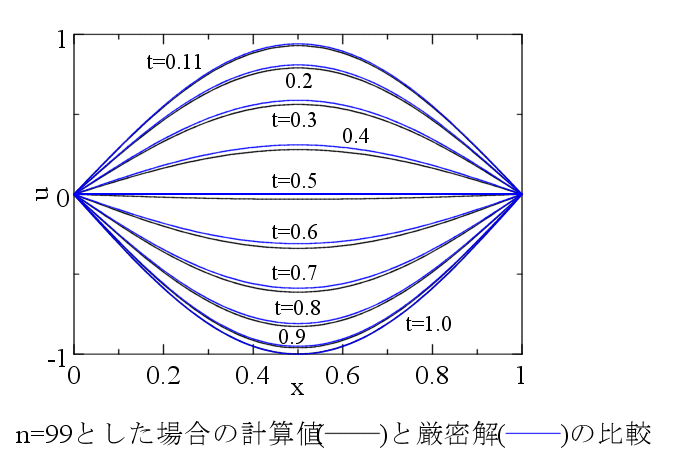
次の図のような結果が得られることを期待しています。
図からわかるとおり，この問題の解は，区間 0≦x≦1 に存在する定在波を表します。上の厳密解の形をみれば，ある区間に張り渡された弦の振動なども，実はその弦に沿って左右に伝播する波動の合成として実現されるものだということが理解できるでしょう。
課題提出
戻る