情報処理及び演習 ＜水曜４限；Ｔ３クラス（塚田・藤本 担当）＞

12月22日&1月12日

常微分方程式の数値解法とそのプログラミング

常微分方程式の解を求める数値計算法について解説し，そのFORTRANプログラミングの実習を行なう。

12月22日の講義

1月12日の課題

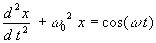
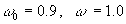
初期条件：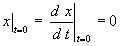

ただし，ルンゲクッタ法（4次）を使いなさい。
なお，各時間ステップにおける計算の部分にサブルーチン副プログラムつかうなど 工夫して下さい。
t=0〜150までの数値解を Excelで図示しなさい。

「ルンゲクッタのおまけ解説はこちら」

補足解説

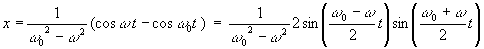
この解のt=0〜150までの時間発展の様子を示すと次のようである。

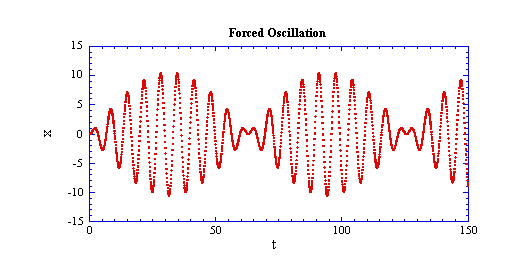
これと比べて，諸君の作ったプログラムによる計算結果は，どれほど正しいであろうか。

1月12日の出席確認

メールで確認することにします。 15：00〜16：00の間に，課題演習の進捗状況をメールで報告してください

• なお，メールのあて先は：　takuya.a@t23x0088.mbox.media.kyoto-u.ac.jp （TA有本君）
• 上記の時間帯以外に到着したメールは，出席と見なしません

1月12日の課題提出について

プログラムと計算結果の図をレポート文書にまとめ，印刷して提出してください。
前回の演習を参考に，きれいなWord文書にしてくれることを期待しています。
なお，ルンゲクッタ法（４次）だけでなくオイラー法（１次）と計算結果を比較する など，工夫をしていただけると最高です。

戻る